Metodika tvorby zaoblení
Návrh zaoblených hran je vždy především strategickou záležitostí. Jedná se o oblast, která může být poměrně často v rozporu z požadavky konstruktéra a je tedy vždy nutné použití zaoblených p…
Návrh zaoblených hran je vždy především strategickou záležitostí. Jedná se o oblast, která může být poměrně často v rozporu z požadavky konstruktéra a je tedy vždy nutné použití zaoblených přechodů vždy pečlivě zvážit. I když modelovací jádro aplikace dokáže v současné době spočítat i složité tvarové problémy, může se stát, že nelze určitý typ rádiu vytvořit. Další řešení tohoto problému je pak již pouze zkušeností konstruktéra a případně jistých ústupků v geometrii navrhované součásti.
Pokusme se tedy v dnešním článku stanovit alespoň několik základních metodických pravidel, jak postupovat při tvorbě zaoblení tak, aby bylo dosaženo co nejsnadnějším postupem požadovaného součásti.
Pravidlo 1., rádius až na posledním místě
Prvním základním pravidlem, které poměrně výrazně eliminuje vznik případných chyb při tvorbě zaoblení je tvorba zaoblení tak, aby leželo jako finální, cílový prvek v prohlížeči modelu. Zaoblení je v tomto případě ovlivněno již cílovou geometrií součásti a nemusí být využíváno jako případná další reference pro konstrukci dalších prvků. Navíc se takto poměrně výrazně usnadňuje dodatečná modifikace rádiusu.
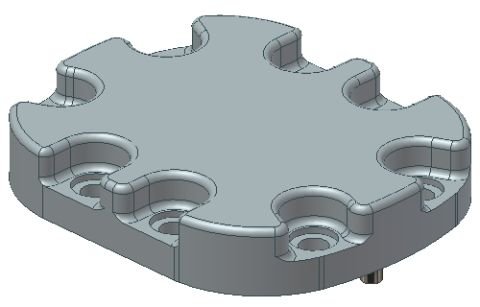
Konstrukce zaoblení na víku
Pravidlo 2., napřed větší, poté menší
Velmi dobrým pravidlem při tvorbě zaoblení je dodržení postupu zaoblování od největšího po nejmenší. Jedná se o postup, kdy jsou v první fázi vytvořena zaoblení rozměrnější, přes která se pak protáhnou zaoblení s menšími poloměry. Obdobné pravidlo platí také při tvorbě proměnlivých zaoblení, kdy se poloměr průběžně mění po délce hrany buď lineárně, nebo kvadraticky.
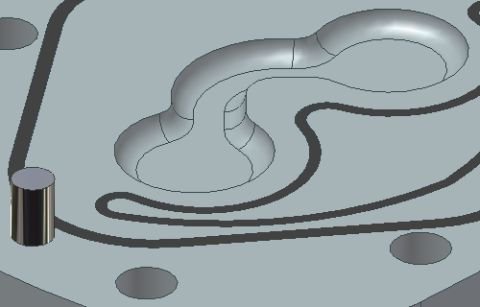
Tvarová, zaoblená drážka
Pravidlo 3., tažený a šablonovaný rádius
V případě, kdy již nelze problém řešit již tradičním konstrukčním prvkem, je možné rádius vytvořit tažením, případně šablonováním prakticky libovolného profilu po hraně profilu. Tento postup je ovšem výrazně složitější a náročnější než tradiční řešení a musí být vždy připraveno potřebné množství trajektorií a profilů pro vytvoření požadovaného tvarového prvku, který je následně odečten od původní součásti a tím vznikne rádius.



