Jak funguje zebra analýza v Inventoru

Zebra analýza, tak lze volně přeložit analyzační nástroj, který má uživatel k dispozici v modulu pro modelování součástí v Autodesk Inventoru. Analýzu lze aktivovat kdykoli v průběhu modelování součástí, nejčastěji v podobě volných ploch. Autodesk Inventor po chvíli vykreslí na povrchu souvislý systém černobílých proužků. Proužky pokrývají plochu jak ze strany záporné, tak ze strany kladné normály, není tedy nutné pro analýzu odvrácené strany plochy tyto normály otáčet.

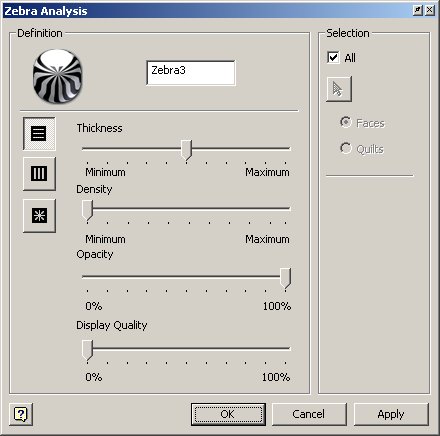
Nastavení zebra analýzy, doporučuji ponechat začínajícím default

Použití zebra analýzy vyžaduje od uživatele trošku cviku a zkušeností, ale její základní požití lze snadno ukázat na jednoduchém příkladě. Jedná se o dvě plochy vytvořené pomocí vyhlazených spline křivek a spojených v jediném bodě. Tento bod lze nejjednodušším způsobem vytvořit pomocí geometrické vazby Totožnost. Plocha je dále vytvořena pomocí běžného vysunutí ve směru normály k rovině tvořící křivky.

Výsledek analýzy je zcela zřetelný z níže uvedeného obrázku. Na první pohled není běžným okem postřehnutelný zlom v napojení dvou spline křivek. Ovšem při aktivaci analýzy je zcela markantní přesazení analyzačního „zebra pruhu“. Ten je specifický právě pro situaci, kdy je analyzován ostrý přechod.

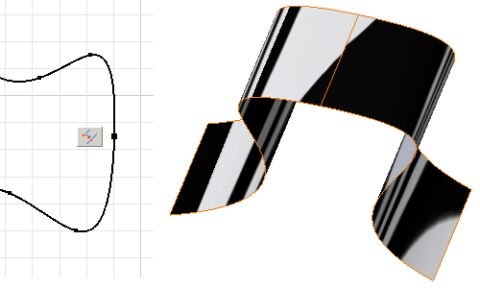
Typický nesymetrický zlom zebry u „ostrého napojení ploch“

Na druhém obrázku je zobrazen druhý případ, kdy je již ovšem použito pro vytvoření napojení dvou křivek kromě vazby totožnost navíc jedenáctkové novinky, vazby pro vytvoření vyhlazeného přechodu úrovně G2. Přechod vytvořený na této úrovni je již zobrazován v zebra analýze bez viditelných posunů podél hranice ploch a lze jej tudíž považovat za čistě provedený. Otázkou jistě zůstává, proč je i v druhém případě zobrazen zlom analyzačního pruhu. Odpověď je jednoduchá, ten je způsoben rozdílnou strmostí pokračování ploch a pruh by byl bez zlomu pouze v případě, že by se jednalo o osově symetrickou záležitost. Rozhodující je ovšem na úrovni G2 jeho posun, nikoli zlom.

Plynulé spojení dvou ploch bez zlomu modifikovaný pomocí vazby Smooth