Vyzkoušejte orientované čáry

V takovýchto případech přichází na řadu nutnost využívat nástroje umožňující zpracování ploch na nízké úrovni. Rády bych připomněl, že velmi zdařilé funkce v této oblasti nemusíte hledat v jiných aplikacích, ale stačí využít buď Mechanical Desktopu, případně Autodesk VIZu. Velmi úzce souvisí tato problematika například s technologiemi rychlé výroby prototypů, které jsou poměrně citlivé na správné orientace povrchových normál, případně na vzájemné přechody ploch.

Mechanical Desktop, o kterých uživatelé často ani neví má v této oblasti řadu užitečných funkcí a je dosažitelný v balíku s Autodesk Inventorem. Poskytuje prakticky komplexní nástroje pro tvorbu a modifikace orientovaných čar s možností přímé vazby na konstrukci drátů a 3D ploch.

Vytvoření orientovaných drátů

Modelování součástí pomocí ploch je poměrně náročným úkolem. Ať se jedná o zpracování ploch získaných například pomocí reverzního inženýrství ze 3D scanneru nebo o plochy vytvářené přímo v Autodesk Inventoru nebo Mechanical Desktopu jedná se vždy o poměrně náročný úkol, který je vždy provázen nutností precizní orientace uživatele v prostoru.

Je nutné si uvědomit to, že v případě modelování ploch neexistuje žádná výrazná možnost zachytávání pracovních případně náčrtových rovin na již existující stěny těles, ale je nutné prakticky vždy vycházet z pracovních rovin, případně ze strategického umístění náčrtů a jejich projekcí na vytvořenou plochu.

Základem principu orientovaných čar je jejich přímá vazba na pozici normály budoucí plochy. Lze tak vytvořit velmi snadno komplexnější systém drátů a pomocí normálových vektorů určit jejich správnou vazbu na budoucí plochu.

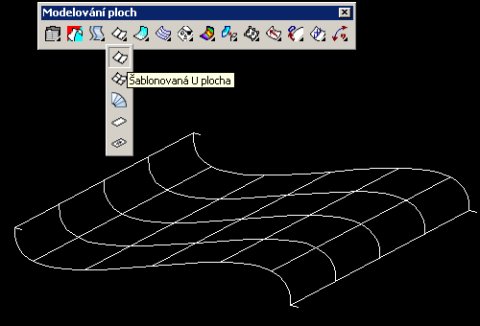
Vliv orientované čáry na tvar plochy

Plochy vytvořené pomocí orientovaných čar lze využít především pro rychlé modifikace tvarově složitějších problémů a jsou velmi efektivní při záplatování tvarových přechodů ploch. V této oblasti poskytují výkonnější řešení než například klasická hraniční záplata, která vychází z okolní křivosti a neumožňuje ji nijak řídit. Plochy lze při editaci přirozeně i analyzovat.