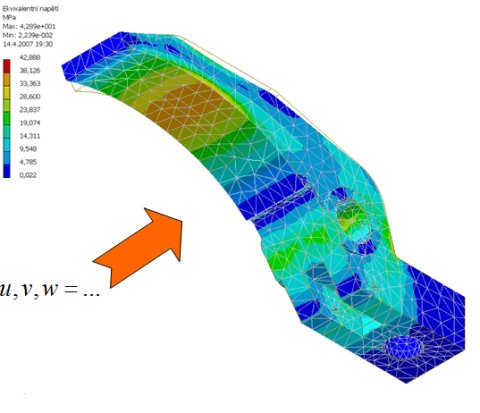
Pevnostní analýza v Autodesk Inventoru Professional 11 – 2. díl, Teorie metody konečných prvků

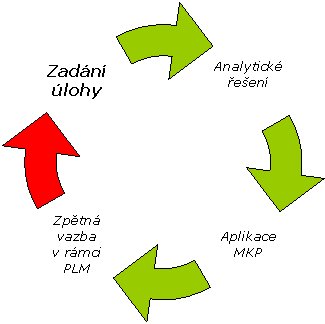
Následující diagram popisuje způsob aplikace metody na daný problém. Ilustruje nejen využití moderních CAE technologií, ale také skutečnost, že není radno bezhlavě věřit všem vypočteným výsledkům. Analytické řešení má i nadále významné místo a lze s jistotou vyslovit závěr, že pokud nemá uživatel dostatečné obecné základy pro řešení daného problému, pak mu není platný ani ten nejlepší MKP systém.

Postřehy k aplikaci MKP v praxi:

-Po zadání vstupních hodnot je provedena rozvaha o možnostech analytického řešení a tedy o případném využití komparace výstupů.

-Dalším krokem je vlastní výpočet pomocí MKP, jehož korektnost je vhodné ověřovat přidáním dalšího kontrolního členu.

-Poslední částí cyklu je zpětná vazba na vstupní hodnoty, kdy do procesu vstupuje dnes již známá zkratka PLM (product lifecycle management) umožňující monitorovat celý životní cyklus strojního uzlu. Ve spojení s MKP to znamená možnost analyzovat napjatost, deformaci a bezpečnost kritického členu ve kterémkolivúdobí jeho funkčnosti.

Matematická teorie metody konečných prvků

Vlastní metoda konečných prvků je definována jako variační metoda, založena na Lagrangeově principu (francouzský matematik Lagrange). Na následujících řádcích je tento princip stručně vysvětlen.

Lagrange principia

Ze všech hodnot posuvů, které neporušují spojitost tělesa a splňují okrajové podmínky se realizují právě ty, které udílí celkové potenciální energii stacionární hodnotu.

Zjednodušeně lze pro následující stav říci, že se hledané posuvy určí jako derivace funkce potenciální energie, která je položena rovno nule. Matematický zápis tedy dán následovně:

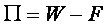
kde Π je celková potenciální energie,

Wje energie napjatosti tělesa,

F je potenciál vnějšího zatížení.

Určení stacionární hodnoty (extrému) je pak dle diferenciálního počtu definováno jako:

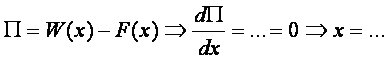
Tímto vyjádřením lze určit všechny neznámé posuvy x.

Čtenář se však jistě ptá, proč jsou vyšetřovány právě posuvy a ne napětí? Ve většině případů určování mechanické napjatosti tuhého tělesa využíváme tzv. deformační přístup metody konečných prvků. Nejprve výpočtem určíme deformaci tělesa a pomocí konstitutivních vztahů (rovnice definující závislost deformace na napjatosti) určíme výsledný průběh napětí viz obr. níže.

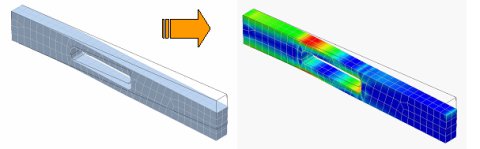
KONCEPCE ŘEŠENÍ KLASICKÉ MKP ÚLOHY

V případě reálného tělesa je však postup komplikovanější. Následující odstavec popisuje, jakými kroky řešení standardní MKP úlohy prochází.

1.Rozklad geometrie na konečný počet prvků

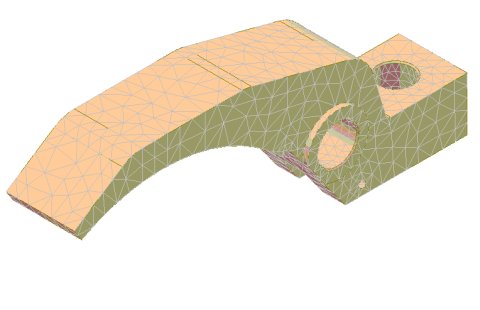
Ve spojení s tímto krokem je důležité zmínit a osvětlit následující pojmy:

Síť – Množina prvků aproximující tvar řešeného tělesa

Prvek – Základní stavební prvek každé sítě. Liší se stupněm, tvarem (čtyřstěn, šestistěn, hranol, pyramida aj.), velikostí, počtem uzlů a bázovou funkcí.

Uzel – Bod prvků, jehož posuv pomocí MKP řešíme (nemusí být ve vrcholech prvku).

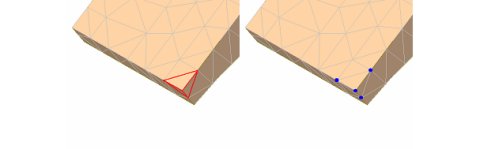
Bázová funkce je v případě MKP definována nad každým prvkem (tím se odlišuje například od Ritzovy metody, kdy je bázová funkce definována nad celým řešeným tělesem. Její bližší význam bude vysvětlen v dalším textu.

2.Sestavení soustavy rovnic

Tvorba sítě je krokem, který je společný pro všechny úlohy MKP. Úkon následující po vytvoření konečnoprvkové sítě je sestavení a řešení samotné soustavy rovnic, na jejímž konci bude nalezení hledané neznámé veličiny. S ohledem na charakter řešené úlohy se již před tvorbou sítě musí uživatel rozhodnout, jaký prvek (tedy i bázovou funkci) zvolí. Odlišujeme prvky pro řešení úloh mechanické napjatosti lineárního a nelineárního charakteru, teplotní napjatosti, elektromagnetismu, mechaniky kontinua aj. Po sestavení dané sítě je pozice každého uzlu vnesena do soustavy rovnic, jejíž tvar je rozličný pro různé úlohy. Následuje přehled některých typů rovnic a vysvětlení diskretizace problému pro případ strojní praxe.

Pro následující úlohy využíváme:

Mechanická napjatost–Rovnice obecné pružnosti

Teplotní napjatost–Laplaceovy rovnice

Elektromagnetismus–Maxwellovy rovnice

Mechanika kontinua–Eulerovy, Navier – Stokesovy rovnice

Diskretizace spojitého problému MKP v případě řešení mechanické napjatosti

Uživatel při řešení deformační varianty, tj. při řešení neznámých posuvů předpokládá výsledek ve tvaru funkcionálu závislého na funkcích posuvů Π (u,v,w). Jeho přímé získání však není matematicky možné (jedná se o nekonečné velkou množinu neznámých posuvů). Proto je do systému vřazena aproximativní veličina tzv. bázová funkce. Součet všech bázových funkcí posuvů (ũ, 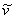,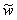) je předem znám a umožňuje přejít od řešení funkcionálu Π (u,v,w) k řešení funkcionálu Π (ai,bj,ck), kde koeficienty ai, bj, ck jsou multiplikativní členy bázových funkcí viz schéma níže.

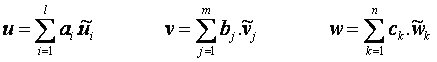
Pomocí Lagrangeova principu jsou pak určeny parametry ai,bj,ck a tím i aproximace hledaných funkcí.

Při dalším rozšířením teorie MKP se lze dopracovat ke všeobecně využívanému výrazu,

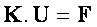
který je běžně využíván v dnešních MKP výpočtech mechanické napjatosti. Tučný označení veličin znamená, že se jedná o maticový zápis, kde

K – je matice tuhosti soustavy (nebo také globální matice tuhosti),

F – určuje matici celkového zatížení,

U – definuje hledanou matici posuvů.

Matice K je při obecné formulaci singulární (determinant je roven nule). V tomto případě výpočet soustavy rovnic není možný. Je proto třeba ji doplnit okrajovými podmínkami, kterými dodefinujeme stupně volnosti uzlů v daných oblastech a tím uzavřeme cyklus potřebný pro řešení úlohy.

Pozn. Při řešení mechaniky kontinua je též užíváno Π funkcionálu, který má však zcela jiný smysl (jedná se o Buckinghemův Π funkcionál).

3.Řešení soustavy rovnic

Rovnice sestavené podle tohoto schématu lze dále řešit některou z numerických metod, jakými může být např. Gaussova eliminace, Gauss – Siedelova metoda, případně různé typy řešičů pro specifické zaplnění matic.

4.Vizualizace výsledků

Jedná se o soubor operací souhrnně označovaní jako post-processing. V rámci tohoto procesu jsou vyřešené hodnoty transformovány do uživatelem preferovaného interface. Většinou se využívá znázornění deformovaných tvarů a znázornění napjatosti pomocí barevných kontur.