Praktické využití funkcí tažení a skořepina

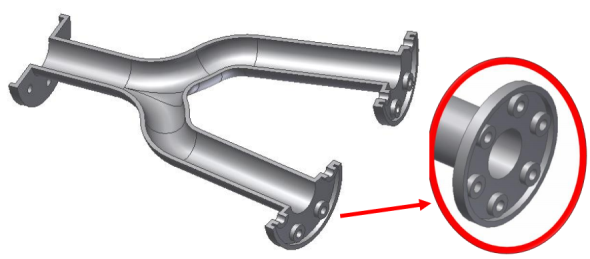
Obě funkce a také další funkce budou demonstrovány na výukovém příkladu části potrubí (Obr. 1), kde je snahou demonstrovat co nejvíce použitých funkcí.

Obr. 1 – toto bude výsledek dnešního snažení

Začneme první funkcí, kterou je funkce tažení. Jedná se o funkci skládající se ze dvou skic. První skica obsahuje křivku tažení a druhá skica obsahuje profil, který je tažen (Obr. 3). Skica taženého profilu musí ležet v rovině, která je kolmá na rovinu obsahující křivkou tažení.  Ideální vždy je, aby jeden koncový bod křivky ležel uprostřed taženého profilu. Tím si zajistíme přehled o tom, kudy bude profil tažen a kde bude mít svůj konec. Aby, se nám s modelem dobře pracovalo, umístíme si první konec křivky tažení i střed profilu do počátku.

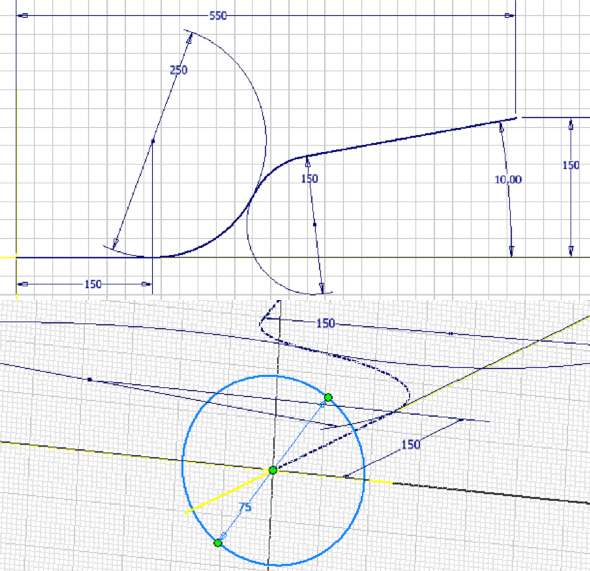
Obr. 2 – nahoře: skica křivky tažení, dole: skica taženého profilu

Následně vybereme funkci tažení, vybereme profil a následně křivku tažení (Obr. 3).

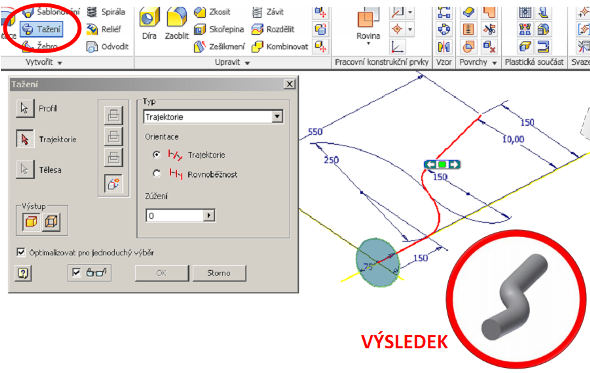
Obr. 3 – funkce tažení

Nyní máme část potrubí, nebo vlastně nemáme, protože vytažený profil není dutý. Nyní můžete namítat, proč jsme nevytáhli rovnou provil obsahují mezikruží (Obr. 4), ale jen kruhový profil.

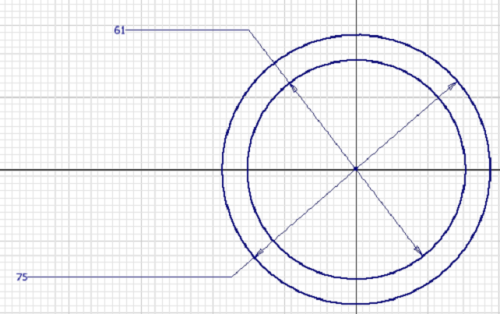
Obr 4. – skica obsahující nepoužitý profil mezikruží

Odpověď je velmi jednoduchá, protože kdybychom toto udělali a následně bychom vytažený profil zrcadlili, dopadlo by to tahle (Obr. 5).

Obr. 5 – výsledek zrcadlení dutého profilu – špatně

Stalo se to, že původní průchozí trubku, jsme protnuli zrcadleným profilem. Naším cílem však je co nejjednodušeji vytvořit potrubní systém, který se z jednoho vstupu bude větvit na dva výstupy, proto budeme pokračovat na původně vytaženém profilu, kterým byla kružnice (Obr. 3). Takto vytažený profil budeme zrcadlit podle roviny, procházející středem (osou) profilu (Obr. 6).

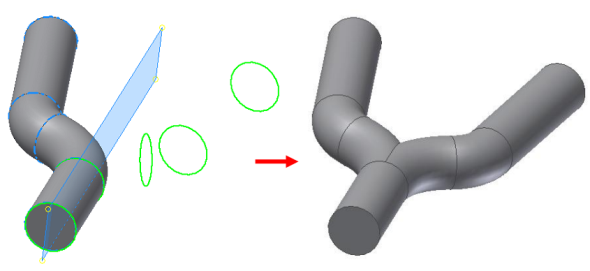
Obr. 6 – po zrcadlení dle roviny symetrie

Nyní je zde otázka, zdali vytvořit z tohoto profilu již potrubní systém, anebo pokračovat ve vytváření modelu dle Obr. 1 a až nakonec vytvořit z plného modelu potrubí. Jelikož chceme vytvořit potrubní systém pomocí funkce skořepina, kterou jsme se zabývali minule, bude tato funkce následujícím krokem (Obr. 7)

Obr. 7 – po aplikaci funkce skořepina

Pro rychlé srovnání, kdybychom použili funkci skořepina až když budeme mít hotový model, dostali bychom následující výsledek (Obr. 8). Výsledek je rozříznutý v polovině, aby bylo jednodušší si představit nevhodnost tohoto řešení.

Obr. 8 – aplikace funkce skořepina až na hotovém modelu – špatně

Nicméně vraťme se k výsledku po aplikaci funkce skořepina, který je na Obr. 7.  Teď si vytvoříme zaoblení v místě, kde se rozděluje potrubní systém na dvě větve (Obr. 9).

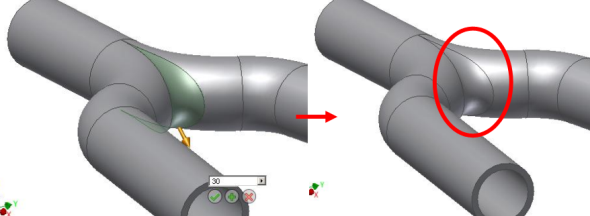
Obr. 9 – zaoblení v místě rozdělení na dvě větve

Otázka, která může nastat, by mohla znít: Proč jsme nejprve nevytvořili zaoblení a teprve poté neaplikovali funkci skořepina? Odpověď je jednoduchá. Uvedené potrubí bychom nejjednodušeji vytvořili svařením tří trubek v místě rozdělení na dvě větve. A dané zaoblení tedy reprezentuje svar a navíc i zesílení v tomto místě, které bude zatížené více než ostatní. Opět musím připomenout náš cíl a to ukázat si funkci tažení v kombinaci s funkcí skořepina. Kdyby toto nebylo naším hlavním cílem, řešili bychom celý model jako sestavu svařence, kterou Inventor taktéž umožňuje (Obr 10). 

Obr. 10 – takto by vypadal potrubní systém jako sestava svařence

Následujícími částmi, které budeme vytvářet, jsou příruby. Vytvoříme skicu na plochu jednoho z mezikruží na straně výstupu. Skicu mezikruží vysuneme funkcí vysunutí (Obr. 11).

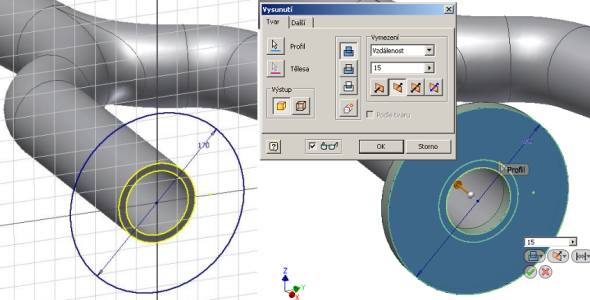
Obr. 11 – vytvořená příruba bez děr

Na plochu příruby si vytvoříme další skicu, do které vložíme bod určující střed jedné děr. Následně použijeme funkci díra. Funkce díra umožňuje vytvářet jednoduché díry, díry s osazení, či závitové díry. Vytvoříme tedy díru se středem v bodě, který jsme vytvořili ve skice. Pro vytvoření zbylých děr použijeme funkci kruhové pole (Obr. 12).

 

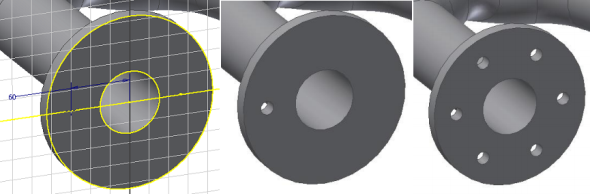
Obr. 12 – funkce díra a funkce kruhové pole

Přírubu na druhém výstupu vytvoříme opět pomocí funkce zrcadlení, kdy opět vybereme rovinu procházející osou symetrie (Obr. 13).

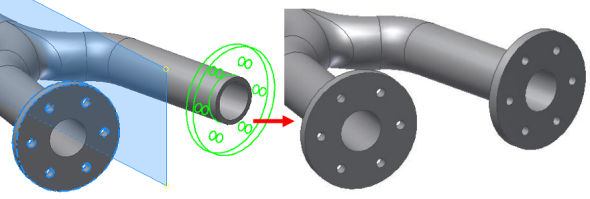
Obr. 13 – vytvoření druhé příruby zrcadlením

Obdobným způsobem vytvoříme i přírubu na vstupu. Jen pro zopakování nejdříve vytvoříme samotnou přírubu pomocí funkce vysunutí, následně jednu díru pomocí funkce díra a poté zbylé díry kruhovým polem (Obr. 14).

Obr. 14 – po vytvoření poslední příruby = výsledek