Pevnostní analýza v AIP 12. díl – Základní statická analýza 9. část
V dnešním díle naše seriálu o pevnostní analýze v Autodesk Inventor Professional si přiblížíme druhy výsledků, které máme k dispozici. Jinými slovy, budeme se bavit o panelu Výsledky, který najdeme v …
V dnešním díle naše seriálu o pevnostní analýze v Autodesk Inventor Professional si přiblížíme druhy výsledků, které máme k dispozici. Jinými slovy, budeme se bavit o panelu Výsledky, který najdeme v modelovém stromě pevnostní analýzy, viz následující obrázek.
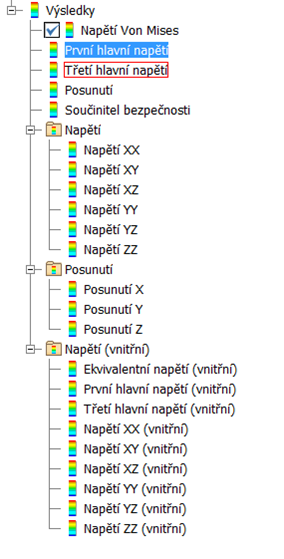
Obr. 1 – Rozbalený panel dostupných výsledků.
Veličiny výsledků, bohužel nejsou i po mnoha letech existence modulu Pevnostní analýzy dokumentovány a mohou být matoucí i pro uživatele, který má již s MKP simulacemi zkušenosti. Proto si je podrobně přiblížíme.
Ještě předtím si připomeňme základní fakta. Pevnostní analýza nám slouží ke zjištění stavu napětí tělesa. Stav napětí je zjišťován pouze v konečném počtu bodů tělesa. V oblastech (objemu) mezi těmito body jsou hodnoty interpolovány. Stav napětí je charakterizován tenzorem 2. řádu, který má pro 3D těleso se třemi nezávislými osami 3 • 3 = 9 složek, viz následující obrázek.
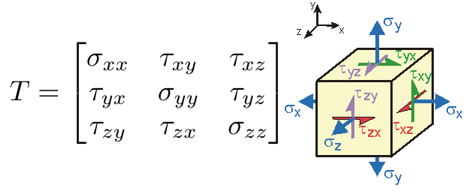
Obr. 2 – Tenzor napětí na nekonečně malém objemu materiálu. Na libovolnou plochu elementu může síla působit ve dvou směrech – kolmo na plochu a rovnoběžně s plochou ve směru 2 zbývajících ortogonálních os.
Jednotlivé složky tenzoru označujeme dvojím způsobem, podle směru působení síly, která na dané ploše napětí způsobuje. Pokud působí kolmo, označujeme ji malým řeckým ?, pokud působí rovnoběžně (tečně), označujeme ji za malým řeckým ?. Tyto napětí se také nazývají jako smyková napětí.
Pokud se pozorně podíváme na Obr. 2, všimneme si, že pro každou osu najdeme dvě souhlasně působící tečná napětí, která jsou identická, pouze je prohozen index. Z toho plyne jeden důležitý fakt – byť má tenzor napětí 9 složek, nezávislých je pouze 6, jinými slovy tenzor napětí je symetrický.
Hodnoty složek tenzoru napětí záleží na mnoha faktorech (materiálový model, zatížení), ale také na volbě souřadnicového systému. Představme si dlouhou, štíhlou tyč, kterou na obou koncích namáháme tahem. Souřadnicový systém můžeme zvolit tak, že osa Z je totožná s osou tyče, při ideálním tahovém zatížení obou konců tyče vzniká pouze jednoosá, kladná (tj. tahová) napjatost ve směru složky ?z. Pokud bychom zvolili souřadnicový systém jinak, elegance jednoosé napjatosti se naruší a napětí se začne rozkládat do všech složek, včetně smykových. K tomu se váže i poslední důležitý fakt, který je potřeba uvést a to, že obecně lze nalézt takové natočení souřadnicového systému, ve kterém budou všechny tečné (smykové) složky tenzoru napětí nulové a ve kterém budou figurovat pouze napětí souhlasné se zvoleným souřadnicovým systémem. Taková napětí nazýváme hlavní a hrají důležitou roli při vyhodnocování bezpečnosti vůči meznímu stavu pružnosti. Lze je totiž porovnávat s materiálovými charakteristikami, které se experimentálně stanovují, tj. tahová/tlaková zkouška, ve kterých se měří pouze jednoosá napjatost bez přítomnosti smykových napětí.
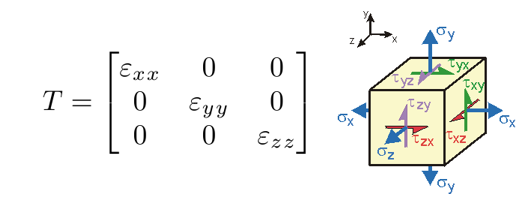
Obr. 3 – Tenzor hlavních napětí. Smykové složky jsou rovny nule a vyskytují se pouze napětí souhlasná se zvoleným souřadnicovým systémem.
Pojďme se tedy podívat na to, co má k dispozici v Inventoru. V základu máme 5 základních položek – Napětí Von Mises, První a Třetí hlavní napětí, Posunutí a Součinitel bezpečnosti, viz následující obrázek.
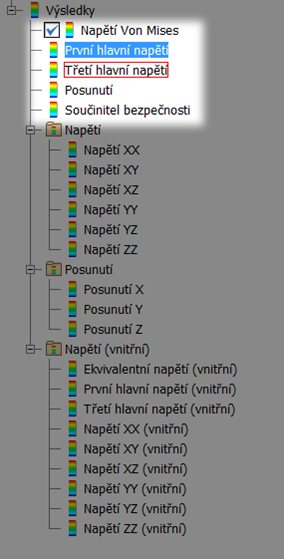
Obr. 4 – Základní položky Výsledků pevnostní analýzy.
Jak jsme si již řekli v 9. dílu našeho seriálu, napětí Von Mises je vhodné pro víceosé namáhání, kde se potřebujeme řídit redukovaným napětím, které je stanovováno podle několika různých předpisů, který lze nalézt zde. Je to základní veličina, o kterou by se měl konstruktér zajímat a ze které je stanovován součinitel bezpečnosti.
První hlavní napětí je vhodné, když potřebujeme sledovat tahovou jednoosou napjatost nezatíženou smykem (viz definice hlavních napětí). Třetí hlavní napětí má charakter čistého tlaku. Tato dvě hlavní napětí jsou také důležitá pro konstrukci Mohrovi kružnice.
Posunutí nám zobrazuje přímé posuvy jednotlivých uzlů a tato veličina je přímým výsledkem MKP analýzy, ostatní veličiny sady výsledků, jsou získávaný z těchto posunutí. Při jejich zkoumání je dobré se přesvědčit, zda jsou reálné. Posuv 0,5 m na ocelové tyči, která má na délku 1 m, asi není v pořádku.
Součinitel bezpečnosti je stanovován podle nastavení v tabulce materiálů a to vůči mezi kluzu (výchozí hodnota), popř. vůči mezi pevnosti materiálu. Jako dělitel ve zlomku pro výpočet bezpečnosti slouží napětí von Mises. Příklad: Pokud uzel modelu napětí von Mises hodnotu napětí Von Mises 100 MPa, použitý materiál modelu má mez kluzu 350 MPa, je součinitel bezpečnosti roven 350 MPa/ 100 MPa = 3,5 (bez jednotky). Hodnoty pod 1 nejsou vůbec přípustné a konstruktér musí v tu chvíli zvážit, zda je výpočet správně a pokud ano, musí přistoupit ke změně designu.
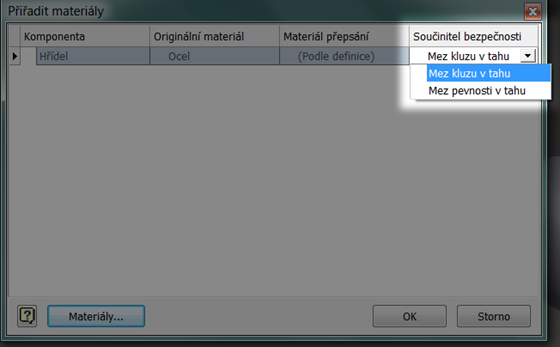
Obr. 5 – Volba kritéria, ke kterému je počítán součinitel bezpečnosti. Mez pevnosti nemá smysl, jelikož Inventor umí pouze lineární elastické materiálové modely, přičemž by se lineární chování předpokládalo až do meze pevnosti v tahu, což je v hrubém rozporu s realitou.
Mimo tyto základní veličiny máme také k dispozici další, jmenovitě to jsou Napětí, Posunutí a Napětí (vnitřní), což velice nešťastný překlad, viz dále. Pokud si rozbalíme složku výsledků Napětí, objevíme zde 6 položek, jmenovitě XX, XY, XZ, YY, YZ, ZZ. Jak asi tušíte, 6 položek je zde právě kvůli symetrii tenzoru napětí, tj. složka tenzoru napětí XY je identická jako YX, XZ stejná jako ZX atd. Nešťastné je zde označení pouze formou názvu a os. Uživatel tak nemůže na první pohled odlišit kolmá (tahová, tlaková) a napětí rovnoběžná (smyková) s rovinou zatížení. Řecká písmena by orientaci prospěla. Jednotkou napětí je MPa.
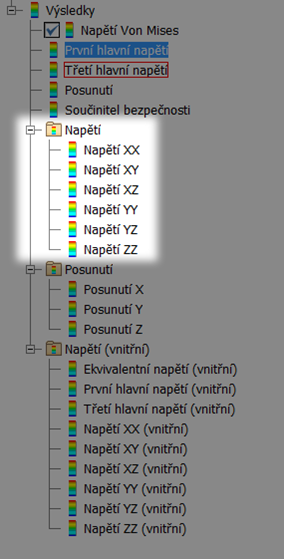
Obr. 6 – Dostupné výsledky tenzoru napětí. Položek je 6, právě kvůli symetrii tenzoru napětí.
Naopak pochopení veličin u složky Posunutí, viz následující obrázek, je bezproblémové. Jednotlivé položky Posunutí X, Y a Z jsou posunutí rozloženy do jednotlivých os. Položka Posunutí, o které jsme se bavili o několik odstavců výše, je stanovena jako skalární součin těchto 3 položek. Jednotkou je mm.
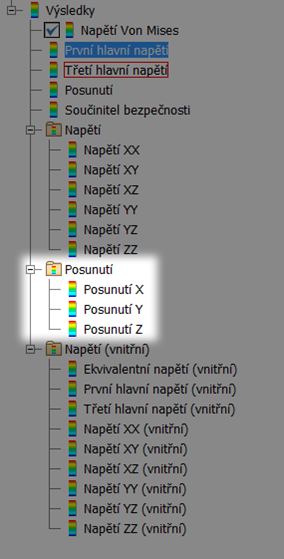
Obr. 7 – Položky posunutí. Ze složek X, Y a Z je pomocí skalárního součinu sestavena položka Posunutí, která je přímo v kořenu výsledků a která je zaznačena na obrázku také.
Poslední položka Napětí (vnitřní) je poměrně nešťastná volba překladu. V originále se jedná o veličinu „Strain“ – Přetvoření. Pro její pochopení je důležité pochopit, jaký je rozdíl mezi posunutím a přetvořením.
Představte si provaz o délce 1 m, který položíte na zem. Tuto polohu označíme jako výchozí. Pokud bychom vzali konce provazu a spojili je tak, že vznikne tvar písmene „O“, proběhla změna polohy – posunutí, ale provaz jako takový jsme nevystavili žádné deformaci. Pokud bychom konce provazu obtočili okolo sloupu, který by nás donutit spojit konce silou, tj. aby se provaz natáhl, provaz jsme přetvořili – způsobili jsme v něm vnitřní změnu napjatosti.
Veličinu přetvoření lze chápat jako poměrnou změnu délky, popř. v objemu v daném směru. Z toho plyne, že se jedná o bezrozměrnou veličinu a že hodnoty kladné určují tahové namáhání, naopak hodnoty záporné určují tlakové namáhání (stlačení). Přetvoření je opět symetrickým tenzorem 2. řádu, proto složka Napětí (vnitřní) obsahuje složky XX, XY, XZ, YY, YZ, ZZ.
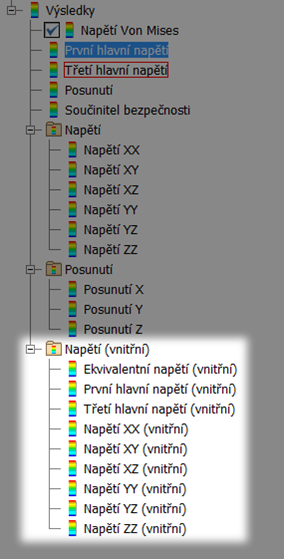
Obr. 8 – Položky Napětí (vnitřní). Tento překlad je matoucí a je potřeba si pamatovat, že se jedná o veličinu přetvoření, která je bezrozměrnou veličinou.
Kromě těchto položek lze zde najít položky Ekvivalentní napětí (vnitřní), První a Třetí hlavní napětí (vnitřní). Položka Ekvivalentní napětí (vnitřní) udává ekvivalentní přetvoření vypočtené podle předpisu von Mises, přičemž z tohoto přetvoření je poté stanoveno napětí von Mises. První a Třetí hlavní napětí (vnitřní) udávají První a Třetí hlavní přetvoření a opět je z nich stanoveno opravdové (ve smyslu významu slova) vnitřní napětí.

Obr. 9 – Tenzor hlavních přetvoření. Opět se jedná o symetrický tenzor, ve kterém jsou pouze 3 složky, nejdůležitější jsou první a třetí, které jsou právě dostupné.
Příště se podíváme na práci se stupnicí výsledků.



